맥 프로, Mac

• 맥 사용
• 한/영 전환 = command + space
• 부트캠프
• 설치
• USB (8G 이상); 윈도우 ISO (64비트) 파일
• 참고 사이트
• Windows 파일 복사중 단계(30분~1시간 소요)
• 부팅
• 전원 구동시 옵션키(opt/option 버튼) 누르고 있기.
• 사용
• 한/영 전환 = 오른쪽 옵션키

그리스 및 로마의 주요 god

• Aphrodite(아프로디테)-그리스 Venus(베누스)-로마 Venus(비너스)
• Apollon(아폴론)-그리스 Phlebus(포에부스)-로마 Apollo(아폴로)
• Arss(아레스)-그리스 Mars(마르스)-로마 Mars(마즈)-영어 화성
• Artemis(아르테미스)-그리스 Diana(디아나)-로마 Diana(다이아나)
• Athena(아테나)-그리스 Minerva(미네르바)-로마 Minerva(미네르바)
• Demeter(데미테르)-그리스 Ceres(케레스)-로마 Ceres(세레스)
• Dionisos(디오니소스)-그리스 Bacchos(바코스)-로마 Bacchrs(바커스)
• Hephaistos(헤파이스토스)-그리스 Vulcan(뷸칸)-로마 Vulcan(불켄)
• Hera(헤라)-그리스 Juno(유노)-로마 Juno(주노)
• Hermes(헤르메스)-그리스 Mercurws(메리쿠리우스)-로마 Mercury(머큐리)
• Poseidon(포세이돈)-그리스 Vulcanus(넵투누스)-로마 Neptune(넵튠)
• Zeus(제우스)-그리스 Jupiter(유피테르)-로마 Jupiter(주피터)

Keras, PyTorch

Keras

• (2017.09.03) Keras shoot-out: TensorFlow vs MXNet
• Keras를 TensorFlow 또는 MXNet 연동하고 각각의 성능을 간단하게 비교 
• API on top of either TensorFlow or Theano
• Primary maintainer is François Chollet, a Google engineer.
• Focused only on deep learning algorithms

1 2 3 4 5 6 7 8

import keras.layers as L import keras.models as M my_input = L.Input(shape=(100,)) intermediate = L.Dense(10, activation='relu')(my_input) my_output = L.Dense(1, activation='softmax')(intermediate) model = M.Model(input=my_input, output=my_output)

cs

PyTorch

• Facebook
• just-in-time graph compilation
• It doesn’t treat graphs as separate and opaque objects. Instead, you can assemble tensor computations ad hoc in very flexible ways.
• 즉, 동적인 연산 그래프(dynamic computation graphs, DCG)를 이용함.
• c.f. Theano 및 TensorFlow는 정적인 연산 그래프를 이용.
• Multi-GPU support, though Tensorflow still wins for larger distributed systems.

Lasagna

Kur

• Deep Learning API 
• supports Theano, TensorFlow, PyTorch
• supports multi-GPU

[Util] pdfdiff, PDF 파일간 비교

pdfdiff

• Command-line tool to inspect the difference between (the text in) two PDF files.
• https://github.com/cascremers/pdfdiff

Information, Entropy

Information

• Claude E. Shannon이 제안한 information theory에서의 information 개념
• '정보량'을 표시하기 위한 추상적인 척도라고 간주하자.
• 확률(함수)을 통해 정의됨
• 주사위  눈금 1이 나올 확률에 대한 정보량 = -log(1/6) = 2.6 (이 때, 로그 밑을 2로 두어 계산했을 때)

$$ h(x) = -log\left \{ p(x) \right \} $$ 

Entropy

• 하나의 system이 가지는 평균 정보량
• 지수가 2인 로그를 사용하여 계산할 경우, 컴퓨터 저장 단위인 bit와 물리적 단위를 일치시킬 수 있음.

$$ H(x) = \sum_{x} p(x)h(x) = -\sum_{x} p(x)log\left \{ p(x) \right \} $$

• Decision Tree를 compact하게 만드는 데 있어, 데이터 분포의 순도(purity)를 나타내는 척도로 활용됨(즉, entropy는 impurity의 척도를 나타냄)
• 데이터 순도가 높을 수록, entropy는 낮아짐. 반대로, 데이터가 많이 혼합되어 있을 수록(즉, tree에 class의 분포가 고르게 퍼져있을 경우) entropy는 높아짐. 
• 혼합성/엔트로피가 작을 수록, 데이터 구별이 더욱 용이해짐.
• Information Gain: 특정 속성을 기준으로 데이터를 구분하게 될 때, '감소되는 entropy의 양'
• Information gain이 커질 수록 더욱 효과적인 데이터 구분이 가능해짐.

KL-divergence

• 두 개의 확률분포(=확률함수) P와 Q가 있을 때, 실제로는 P에서 나온 데이터가 다른 확률함수 Q에서 나왔다고 가정할 경우 발생하는 추가 정보량으로 해석할 수 있음.
• 즉, 두 확률분포의 엔트로피 차이를 나타내는 준 거리 공식(semi-distance)
• $D_{KL}(P,Q) = D_{KL}(P||Q) = \sum_{i} p_{i}log\frac{p_i}{q_i}$
• 두 확률분포 사이의 거리 측정에 활용됨.
• KL은 대칭성(symmetry)을 만족하지 못하기 때문에, 실제로 손실 공식으로 사용하기 위해서는 p가 실제 라벨인지 q가 실제 라벨인지 구별해야 함.
• 머신러닝에선 p를 실제 정답인 라벨로, q를 예측한 확률분포로 사용함. (q가 0이 될 경우의 분모가 0이 될 지도 모른다고 걱정할 수 있는데, 만약 예측이 지수 정규화(softmax) 활성함수(activation function)의 결과물이라면 q가 0이 될 일은 없다고 함.)
• 참고: 함수 d(x,y)가 metric이 되기 위해 필요한 특성 4가지
• d(x,y) >=0
• d(x,y) = 0 iff x==y
• d(x,y) = d(y,x)
• d(x,z) <= d(x,y) + d(y,z)
• KL divergence는 q에 대한 convex function이며, p는 실제 확률분포로 주어질 때, KL 거리를 최소화하기 위한 식에서 고정값으로 간주할 수 있음.
• $minimize(D_{KL})=minimize(\sum_{i} p_{i}logp_i-\sum_{i} p_{i}logq_i)=maximize(\sum_{i} p_{i}logq_i) = minimize(-\sum_{i} p_{i}logq_i)$

Cross-entropy (교차 엔트로피) 

• = $-\sum_{i} p_{i}logq_i$ = negative log-likelihood (음수 로그 유사도)
• 만약 y가 0 또는 1 값만 가지는 경우, Cross-entropy를 이용한 loss function은 다음과 같이 표현 가능
• $ L=-ylog\hat{y}-(1-y)log(1-\hat{y})$
• y가 여러 클래스를 갖는 경우의 loss function
• $ L=-\sum_{i}ylog\hat{y}$

Probabilistic Data Structure

Probabilistic Data Structure

Objective

• 확률적 데이터 구조를 이용한 근삿값을 연산함으로써, 메모리 사용량 낮추고, 실시간 데이터 처리하되, 약간의 오차를 허용한 결과값을 얻는 방식.
• (random 함수가 아니라) 주로 hash 함수를 이용하여, 데이터 유일성 판단에 대해 확률적으로 접근함
• 예를 들어, 
• Memebership Query: 주어진 element가 특정 set의 member 여부에 대한 판단.
• Cardinality: 주어진 set 내의 유일한 element 개수를 연산.
• (Top-K/Range) Frequency: 중복을 포함하는 set에서 특정 element가 몇개나 포함되어 있는 지 판단.
• 연관된 개념: 
• Universal approximation theorem
• artificial neural network의 수학적 이론에 의하면, finite number of neurons을 포함하는 single hidden layer를 가진 feed forward network은 continuous function으로 approximate 될 수 있음을 의미함; 즉, 단순해 보이는 NN이지만 appropriate paramter에 의해 다양한 함수를 표현 가능하다는 의미임.  

(Approximate) Membership Query

• Wiki: 주어진 element가 특정 set의 member인지를 테스트하기 위한 필터. 
• 데이터베이스에 해당 key가 존재하는 지 확인(lookup)하기 위한 proxy로 주로 사용됨.
• 응용 설명
• Bloom Filter
• (Bloom, 1970)에 의해 제안된, AMQ에 관한 space-efficient 확률적 데이터 구조.
• False negative 발생하지 않는 것을 보장하지만, False positive는 발생 가능.
• 예를 들어, 데이터베이스에 존재하지 않는 데이터에 대한 disk lookup을 reduce하거나, 웹브라우저에서 malicious URL을 식별한다거나, 비트코인 wallet synchronization에 이용됨.
• 0으로 채워진 m개의 bit array에 대해, k개의(이 때, k<m) 서로 다른 hash function을 이용하여, element의 hash 값을 uniform random 분포를 통해 array 위치마다 1로 설정; 만약, 주어진 element에 대한 k개의 hash 값을 살펴보았을 때, 
• 1) 필터값이 어느하나라도 0인 경우가 존재한다면, 해당 element가 set에 속하지 않는다고 판단할 수 있음. 
• 2) 필터값이 모두 1인 경우, set에 포함된다고 판단 가능
• simple Bloom Filter는 false negative를 허용하지 않기 때문에, 원소 삭제(element removal)가 기본적으로 불가능함; 집합 내의 원소 개수가 늘어날 수록, false positive 발생 확률도 증가함.
• 관련 개념: 
• Feature hashing (=hashing trick): 기계학습에서, feature를 vector(또는 matrix)로 변환(vectorizing)하는 빠르고 공간 효율적인 방안; Bag of Words(BOW)이나, Term-Document Matrix를 표현함에 있어, hash 함수를 이용한 indices 도출.
• MinHash (=min-wise independent permutations locality sensitive hashing scheme): (Broder, 1997). 중복 웹 페이지 조회 결과를 제거하기 위한 방안. Association Rule Learning 등에 이용됨.
• Skip list: ordered linked list를 이용해서, fast search를 하기 위한 자료 구조.
• Counting (Bloom) Filters
• (Fan, 2000)에 의해 제안됨; Bloom Filter의 delete operation 구현 방안 제공.
• 필터를 재생성하지 않고도 원소의 삭제가 가능하도록, array내 각 bucket의 크기를 1비트에서 n비트로 확장하여, counter로 사용. (즉, Bloom Filter는 array bucket size가 1비트인 Counting Filter로 간주할 수 있음.)
• element가 추가될 때마다, bucket의 값을 1씩 증가시키고, 삭제될 때마다 1씩 감소시킴
• bucket의 overflow를 방지하기 위해서, 충분히 큰 data type 및 최댓값 설정이 필요.
• 그러나 기존 정적 Bloom Filter에 비해, n배 더 많은 메모리 공간을 사용하게 됨; 또한 테이블의 크기가 여전히 고정되어야 하므로, 수용 범위를 넘어선 element가 추가되기 시작하면, false positive 확률이 증가하게 됨. 
• Quotient Filter
• (Bender, 2011)에 의해 제안된, AMQ에 관한 space-efficient 확률적 데이터 구조.
• 주어진 element가 특정 set에 절대로 포함되지 않는 지, 또는 해당 set에 probably 포함될 지에 대해서 질의 수행 가능.
• False negative 발생하지 않으나, False positive는 확률적으로 발생 가능.

Cardinality

• HyperLogLog
• (Flajolet, 2007)에 의해 제안됨.
• 매우 적은 메모리로 집합의 원소 개수(Cardinality)를 추정할 수 있는 방법; 

Frequency

• Count–min sketch
• (G. Cormode, S. Muthukrishnan, 2003) 제안; frequency 추정을 위한 확률적 데이터 구조.
• 정확한 빈도값을 계산하려면, HashMap을 이용해야 하지만(이 때, 원소 개수에 비례하는 메모리 공간 필요), 더 적은 메모리 공간(sublinear space)을 이용하여 근삿값에 의하여 빈도수를 계산함
• 전체 원소 중에 극히 일부만 빈도 값이 큰 분포를 다루기에 적합.
• Counting Filter와 본질적으로 동일한 자료 구조이지만, 다른 방식으로 활용된다고도 해석됨.

Google cloud

Google cloud tutorial

• Tutorial
• http://cs231n.github.io/gce-tutorial/
• http://cs231n.github.io/gce-tutorial-gpus/

Public Dataset

• amazon의 대용량 공간 데이터 집합
• 구글 클라우드 플랫폼 데이터 집합
• https://cloud.google.com/bigquery/public-data/
• 마이크로소프트 sample datasets in Azure Machine Learning Studio

• Awesome Public Datasets 
• 공개된 데이터 집합들을 정리한 사이트. 
• Real-world data sets collected from the web 
• Book: <Introduction to Programming in Java>과 연관된 데이터 집합들.
• Webster's New International Dictionary, Second Edition (as known as Webster's NI2 dictionary)
• Web2.txt = Single words – 234,936 entries 
• The first publication of this dictionary, also called NI2 or Webster's 2nd, came in 1934, but revised editions were issued over the next couple decades.
• News Aggregator Data Set
• 2016.02.28에 donation된 데이터
• 뉴스 웹 페이지에 대한 참조 URL들이 포함됨.
• 전체 데이터 인스턴스 개수는 422937
• UCI Machine Learning Repository
• UCR 시계열 데이터 집합
• Kaggle'sopen data platform
• 기상청 국가기후데이터센터
• AudioSet
• label이 모두 달린 오디오 데이터.
• expanding ontology of 632 audio event classes and a collection of 2,084,320 human-labeled 10-second sound clips drawn from YouTube videos.

IT Company Interview

Coding Interview

• Coderust 2.0 (유료)
• Faster Coding Interview Preparation using Interactive Visualizations
• 80 programming interview questions with step-by-step visual explanations provide learners a faster way to prepare for coding interviews. Solutions are available in C++, Java, Python, Javascript, and Ruby.
• LeetCode 

System Design Interview (SDI)

• Grokking the System Design Interview (유료)

Variational Inference

VAE 논문을 읽다가 해당 개념을 찾아보게 되었다.

• 목적: 
• to approximate an intractable probability distribution, $p$, with a tractable(다루기 쉬운) one, $q$, in a way that makes them as ‘close’ as possible.
• 복잡한 분포(distribution)을 조금 더 간단한 형태의 분포로 근사하여 쉽게 풀어보자는 것.
• observation data가 주어져 있을 때 hypothesis에 대한 latent variable을 찾아야 하는 통계적 추론 문제(statistical inference problem)를 최적화 문제(optimization problem)로 re-write할 수 있다는 의미가 있음.
• DL과의 연계성 측면: 대량 데이터의 다차원 공간에 대해 (경사 하강법 등 이용해서) 최적화 문제를 잘 풀 수 있다.
• 이름의 어원: 
• posterior(사후 확률 분포)를 가장 잘 설명하는 특정 분포를 찾아나가는(calculus of variations) 과정.
• 참고: Quora Answer (by S. Wang, 2015 Mar.)
• {세미나 시간에 질문자가 던진 꽤 어려운 질문이 있을 때, 발표자가 해당 질문을 손쉽게 conveniently reframe함으로써, 원래의 어려운 질문을 직접 대답하는 대신 reformulated question에 정확한 답을 주는 상황}을 떠올려 보자.
• 참고: Variational Methods 소개(by E. Jang, 2016 Aug.)
• 수식 표기가 정확하고, 개념적으로 친절하게 설명되어 있음
• 고양이 이미지 분류 예시를 통해 posterior, likelihood 설명함.
• 참고자료: 확률에 대한 개념 요약
• 기계학습에 확률 $p(x)$을 도입하기 위해서는 실수 벡터를 입력으로 받아서 실수값을 출력하는 '함수'로 간주하면 조금 더 이해가 편할 것으로 생각됨; 따라서 distribution 또한 어떠한 파라미터를 가진 확률 함수 $p(x;\theta)$로 볼 수 있을 듯. 

통계/수학 문제에서 posterior를 직접 계산하기 어려운 경우가 많다. (because the normalization constant is intractable.) 즉, $X$가 observation 집합, $Z$가 latent variable 집합을 나타낸다고 하면, posterior $P(Z|X)$를 구하고 싶지만, 다음 식의 분모(denominator) 부분을 직접 계산하기 어려울 때가 많다.

$$P(Z|X)=\frac{P(Z,X)}{\int_{Z}P(Z,X)}$$

• 접근 방안 1: MCMC를 이용해서 샘플링을 하는 방식; 만약 샘플링을 해야하는 parameter 개수가 많아질 경우, convergence가 매우 느려진다(slow to converge).
• Markov chain Monte Carlo
• 접근 방안 2: true posterior $P(Z|X)$를 approximate함으로써 손쉽게 계산한다. 이때, $V$를 approximate variational distribution의 parameter라고 하면 다음의 식으로 표현된다.
• Bayesian model의 posterior distribution에 variational inference를 적용하는 것을 variational Bayes (VB)라고 부르기도 한단다.
• a family of techniques for approximating intractable integrals arising in Bayesian inference and machine learning

$$P(Z|X)\approx Q(Z|V)=\prod_{i}Q(Z_{i}|V_{i})$$

• 여기에서, (실제로 latent variables $Z$는 $X$와 independent하지 않을 수도 있지만,) 'mean field' approximation(평균 장 어림법, 평균 장 점근법)을 전제한다면(to restrict the family of variational distributions to a distribution that factorizes over each variable in $Z$), 문제를 더욱 쉽게 계산할 수 있다. 
• $Z$가 서로 겹치지 않는(independent) 부분 집합 ${Z_1, \dots, Z_M}$으로 구성되어 있을 때, 전체 $Q(Z)$ 또한 각 부분집합의 $Q(Z_i)$으로 factorization 된다는 가정

$$Q(Z|V)=\prod_{i=1}^{M}Q(Z_i|V_i)$$

이제, Kullback Leibler (KL) divergence를 이용해서, $Q(Z|V)$가 최대한 $P(Z|X)$에 가까워지는 $V_{i}$를 계산할 수 있다.

$$\begin{eqnarray*}
V^{*} &=& arg\min_V D_{KL}(Q(Z|V)||P(Z|X)) \\
&=& arg \min_V \sum Q(Z|V)log\frac{Q(Z|V)}{P(Z|X)}
\end{eqnarray*} $$

따라서, estimation 문제가 최소값을 찾아야하는 optimization 문제로 바뀌었고, $V^{*}$를 찾게되면, $Q(Z|V^{*})$를 posterior에 대한 best guess로 사용하도록 한다.

• 참고: KL divergence 관련된 수식들
• KL divergence 를 중심으로 decompose하면 다음과 같다.

$$ \begin{eqnarray*}
D_{KL}(Q||P) &\equiv& \int Q(Z)log\frac{Q(Z)}{P(Z|X)} = \mathbb{E}_Q(log\frac{Q(Z)}{P(Z|X)})\\
&=& \int Q(Z)log\frac{Q(Z)}{P(Z,X)} +\int Q(Z)log(P(X)) \\
&=& \int Q(Z)log\frac{Q(Z)}{P(Z,X)} + log(P(X))
\end{eqnarray*}$$

• $log(P(X))$를 중심으로 decompose하면 다음과 같다.

$$\begin{eqnarray*}
log (P(X)) &=& log\frac{P(Z,X)}{P(Z|X)} \\
&=& log\frac{Q(Z)}{P(Z|X)}+log\frac{P(Z,X)}{Q(Z)}
\end{eqnarray*}$$

$$\mathbb{E}_Q(log (P(X))) = \mathbb{E}_Q(log\frac{Q(Z)}{P(Z|X)}+log\frac{P(Z,X)}{Q(Z)})$$

• $log(P(X))$는 Q(Z)에 대해서 constant 하므로 다음과 같이 표현된다. 또한, $D_{KL}$은 nonnegative이므로, 두번째 항이 $log(P(X))$의 lower bound 또는 ELBO (evidence lower bound) $\mathcal{L}$라고 불린다. 그리고, 첫번째 항을 최소화하기 위해서는 결국 두번째 항을 최대화할 필요가 있다.

$$\begin{eqnarray*}
log (P(X)) &=& D_{KL}(Q||P) + \mathbb{E}_Q(log\frac{P(Z,X)}{Q(Z)}) \\
&=& D_{KL}(Q||P) + \mathcal{L}
\end{eqnarray*}$$

• 이제, ELBO $\mathcal{L}$은 다음과 같이 전개된다.

$$\begin{eqnarray*}
\mathcal{L} &=& \mathbb{E}_Q ( \log{P(Z,X)} -\log{Q(Z)}) ) \\
&=& \mathbb{E}_Q ( \log{P(X|Z)} + \log{P(Z)} -\log{Q(Z)}) ) \\
&=& \mathbb{E}_Q ( \log{P(X|Z)} + \log{\frac{P(Z)}{Q(Z)}} ) \\
&=& \mathbb{E}_Q ( \log{P(X|Z)} ) + \int Q(Z)log\frac{P(Z)}{Q(Z)}
\end{eqnarray*}$$

Bayesian Data Analysis

Bayes’ Theorem

$$P(H|D)=\frac{P(D|H)P(H)}{P(D)}$$

• H: Hypothesis
• D: Data
• P(H): Prior. =사전정보 or 선입견
• P(D): Evidence ~ constant
• P(D|H): Likelihood
• P(H|D): Posterior
• 데이터(관찰값)가 주어졌을 때의 이론(모델)에 대한 확률. 

$$P(H|D)\propto P(D|H)P(H)$$

Maximum Likelihood Estimation (MLE)

• 관찰값 $X = (x_1, x_2, x_3, \ldots, x_n)$가 알려지지 않은 PDF(확률 밀도 함수) $f$에 의해서 생성된 데이터라고 생각하자.
• 즉, PDF $f(X|\theta)$는 a function of parameters ($\theta$) with fixed data ($X$)이면서 likelihood function $f(X|\theta)=\mathcal L(\theta;X)$으로 볼 수 있음.
    
• MLE는 $f$의 파라메터 $\theta$를 estimate함에 있어서, likelihood $\mathcal L(\theta;X)$를 최대로 만드는 $\theta$를 찾는 방법임. 즉, $\theta$가 주어진 상태에서의 데이터들의 확률을 최대화함

$$\hat \theta = \arg\max_\theta \mathcal L (\theta;X) = \arg\max_\theta f(X|\theta)$$

• 이때, i.i.d.(independent and identical distributed) observation을 고려하면, $f(X|\theta) = \prod_i f(x_i|\theta) = \prod_i\mathcal L (\theta;x_i)$가 되며, 일반적으로 단조증가함수인 log를 활용하여 덧셈꼴을 만들고 log likelihood를 통해 $\theta$를 estimate한다.
• 단점: 주어진 observation에 따라, MLE 계산 결과가 민감하게 변할 수 있음. 
• 쉽게 설명하고 있는 참고 글들
• 블로그1

Maximum a Posteriori Estimation (MAP)

• (Bayes' Theorem을 이용해서,) 주어진 데이터 $X$에 대해 최대 확률($f(\theta|X)$)을 내는 $\theta$를 estimate한다.
• $f(\theta)$: Prior
• $\arg\max_\theta f(\theta|X)$: Likelihood
• $f(\theta|X)$: Posterior

$$\arg\max_\theta f(\theta|X)=\arg\max_\theta \frac{f(X|\theta) f(\theta)}{f(X)} = \arg\max_\theta \frac{\mathcal L (\theta;X) f(\theta)}{f(X)}=\arg\max_\theta \mathcal L (\theta;X) f(\theta)$$

• 따라서, Prior $f(\theta)$가 고정 상수라면 MLE와 MAP는 같은 결과가 나오겠지만, 그렇지 않은 경우, 데이터에 대한 사전정보를 이용함으로써 보다 좋은 선택을 할 수'도' 있겠다는 개념임.(=잘못된 선입견을 가질 경우 나쁜 선택을 할 수도 있음)

CNTK

CNTK

• (2017.05.30) https://docs.microsoft.com/en-us/cognitive-toolkit/reasons-to-switch-from-tensorflow-to-cntk
• Tensorflow 대비 MS의 CNTK가 갖는 장점을 설명
• (참고할 만한 기사) http://www.ciokorea.com/news/34465
• 스파크 처리 프레임워크 등을 직접 통합할 수 있는 자바 API를 제공
• 텐서플로의 프론트엔드인 케라스(Keras) 같은 인기 신경망 라이브러리용 코드를 지원
• 저수준과 고수준 기능을 지원하는 파이썬 API를 제공

Data preprocessing, preparation

개념 설명

• https://www.analyticsvidhya.com/blog/2016/01/guide-data-exploration
• 개략적으로 주요 개념들 정리
• http://www.dodomira.com/2016/10/20/how_to_eda/
• 한글로 개념 소개
• 
  

Backpropagation

Backpropagation

• 배경설명
• 이미 1970년대 소개되었으나, 1986년 논문(by David Rumelhart, Geoffrey Hinton, and Ronald Williams.)이 나오기 전까지 중요성이 인지되지 않았음. 
• backpropagation works far faster than earlier approaches.
• 목적: 특정 입력값이 최종 결과에 얼마만큼의 영향을 미치는 지 계산하기 위해.
• Reverse-mode differentiation에 대한 쉽고 친절한 설명
• 약간은 수식이 많고 난해한 설명이지만 참고 가능.
• Ranzato, DL tutorial@CVPR2014 (2014 June)
• Softmax loss function에 대한 derivative

$$L = -\sum_j y_j \log p_j, \\
p_j = \frac{e^{o_j}}{\sum_k e^{o_k}},$$ where $o$ is a vector.
$$\frac{\partial p_j}{\partial o_i} = p_i(1 - p_i),\quad i = j$$
and
$$ \frac{\partial p_j}{\partial o_i} = -p_i p_j,\quad i \neq j.$$
$$ \begin{eqnarray*}
\frac{\partial L}{\partial o_i} &=& -\sum_ky_k\frac{\partial \log p_k}{\partial o_i}=-\sum_ky_k\frac{1}{p_k}\frac{\partial p_k}{\partial o_i}\\
&=&-y_i(1-p_i)-\sum_{k\neq i}y_k\frac{1}{p_k}({{-p_kp_i}})\\
&=&-y_i(1-p_i)+\sum_{k\neq i}y_k({{p_i}})\\
&=&-y_i+y_ip_i+\sum_{k\neq i}y_k({p_i})\\
&=&p_i\left(\sum_ky_k\right)-y_i\\
&=&p_i-y_i
\end{eqnarray*} $$

또는 다음과 같이 표현되기도 함.
$$ \frac{\partial L_i }{ \partial f_k } = p_k - \mathbb{1}(y_i = k) $$
(즉, 정확한 라벨(k)에 대한 score 값에 대해서, 해당 도출된 확률($p_k$)의 역을 이용해서 gradient가 표시되며, 이는 loss를 줄일 수 있는 방향을 나타낸다는 직관적인 해석 가능.)

• sigmoid function에 대한 derivative

$$ \frac{dy}{dx}= y(1-y) $$

• CS231n에서 나온 binary logistic regression classifier의 log likelihood 관련 loss function에 대한 derivative 계산

$$ L_i = \sum_j y_{ij} \log(\sigma(f_j)) + (1 - y_{ij}) \log(1 - \sigma(f_j)), $$ where $\sigma(\cdot)$ is the sigmoid function.

$$ \begin{eqnarray*}
L_i &=& \sum_j y_{ij} \log(\frac{1}{1+e^{-f_j}}) + (1 - y_{ij}) \log(1 - \frac{1}{1+e^{-f_j}})\\
&=& \sum_j (-1)y_{ij} \log(1+e^{-f_j}) + (1 - y_{ij})(\log(e^{-f_j}) - \log(1+e^{-f_j}))\\
&=& \sum_j (-1)y_{ij} \log(1+e^{-f_j}) + (1 - y_{ij})(-f_j) + (y_{ij} -1)\log(1+e^{-f_j}))\\
&=& \sum_j f_j(y_{ij}-1) + (-1)\log(1+e^{-f_j}))\\
&=& \sum_j f_jy_{ij} + (-1)(f_j+\log(1+e^{-f_j}))\\
&=& \sum_j f_jy_{ij} + (-1)\log(e^{f_j}+1)
\end{eqnarray*} $$
Therefore,
$$ \begin{eqnarray*}
\frac{\partial L_i}{\partial f_j} &=& \sum_j y_{ij} + (-1)\frac{1}{e^{f_j}+1}(e^{f_j})\\
&=&\sum_j y_{ij} + (-1)\frac{1}{1 + \frac{1}{e^{f_j}}}\\
&=& \sum_j y_{ij} + (-1)\frac{1}{1 + e^{-f_j}} \\
&=& \sum_j y_{ij} - \sigma(f_j)
\end{eqnarray*} $$

CNN, Convolution

Convolutional Neural Network

Background

• 기존 다계층 신경망(MLP, multi-layered NN)의 문제점
• 입력데이터가 조금만 달라지더라도(이미지 크기 변화; 회전; 변형 등), 새로운 학습을 하기 않으면 좋은 성능이 나오지 않음
• 따라서 많은 raw data로 이루어진 학습 데이터를 매번 학습하기에는 많은 자원 및 시간 소요.
• Training Time; Network Size; Number of free parameters
• 종래 MLP는 입력 이미지의 모든 픽셀 값이 위치에 상관없이 동일 수준의 중요도를 갖는다고 전제함. 
• 이러한 이미지에서의 공간적 데이터 특징(즉, local receptive field)을 무시하여 fully connected network을 이용할 경우, free parameter(즉, weight, bias)의 개수가 많아지고, overfitting 가능성이 높아짐.
• CNN에서는 visual cortex(시각 대뇌 피질)을 본따, 이미지 내의 픽셀들이 그 주변에 있는(즉, 공간적으로 인접한) 픽셀들과만 연관성이 높을 뿐(locality = local connectivity)이며, 그것을 느낄 수 있는 수용영역(receptive field)의 크기가 제한적이라는 점을 활용하고 있음.
• CNN이 갖는 특징
• 공간적으로 인접한 신호들에 대한 correlation 관계(locality)를 비선형 필터(=convolutional kernel)를 이용하여 추출
• 여러 개의 필터를 적용함으로써 다양한 local 특징(=feature map) 추출 가능
• Subsampling(pooling)을 통해 입력 데이터 크기를 줄여나감; 반복적인 필터링과 결합함으로써 global feature를 얻을 수 있음
• 이 때, 전체 입력에 대해 적용하는 free parameter(weight, bias) 공유를 통해 parameter 수를 줄여서 학습시간 및 overfitting을 낮춤
• 즉, 입력 데이터의 위상(topology) 변화에 무관한(또는 강인한) 항상성(invariance) 있는 특징(salient feature)을 도출할 수 있음.
• 그러나, CNN 역시 depth가 깊어지게 되면 다음의 문제를 겪게됨.
• vanishing/exploding gradient로 인해 학습 속도 떨어짐.
• 파라미터 수의 증가로 인한 overfitting 가능성 및 에러 발생 높아짐.

Concepts

Terms

• convolutional kernel = filter = patch
• receptive field
• 정보처리와 관계되는 세포에 대해 응답을 일으키는 자극의 영역. 외부 자극이 전체적인 영향을 주는 것이 아니라, 특정 영역에만 영향을 준다는 의미.
• ConvNet 관점에서 receptive field의 크기 = kernel의 크기 = w x h x d

Convolution

• 특정 시스템에 입력이 가해졌을 때 시스템의 반응이 어떻게 변하는지 해석하기 위한 용도; 이미지에서 특정 feature를 추출하기 위한 필터 구현시 사용됨.
• 참조 문헌
• Understanding Convolutions (2014. July)
• convolution 개념 및 수식 이해 쉽게 설명
• Deconvolution and Checkerboard Artifacts (2016. Oct.)
• convolution filter의 stride, size를 동적으로 조절해볼 수 있음
• Python을 이용한 기본적인 convolution 개념 실습

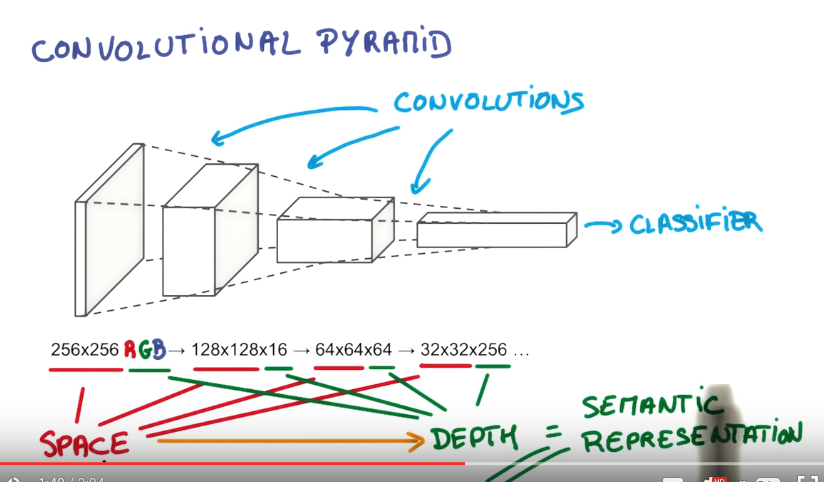
• 1x1 convolution
• C2개의 feature map을 그보다 적은 수의 C3개의 (즉, C2>C3) feature map으로 줄일 수 있어 다음 단계에서 처리해야 하는 파라미터 개수(=연산량)을 감소시킬 수 있음
• 단순한 matrix multiply를 적용할 수 있게 되어 더 빠른 계산 가능

CNN Basic

• Conv Nets: A Modular Perspective (2014. July): [매우 친절한 설명]
• convolutional layer: 입력 데이터를 특정 segment 별로 살펴봐서, certain features를 찾는 과정.
• pooling layer: 직전 layer의 small blocks에서의 feature를 병합
• max-pooling layer: kind of “zoom out”; takes the maximum of features over small blocks of a previous layer. The output tells us if a feature was present in a region of the previous layer, but not precisely where.
• ConvNet Layers and Architectures
• 개략적인 설명.
• Michael Nielsen's book chapter 6. Deep learning
• CNN의 세부적인 개념 설명.

CNN hyper-parameter

• Filter = convolutional kernel
• 필터의 개수
• (시스템의 균형을 잡아준다는 의미에서,) 각 layer에서의 연산 시간/량을 일정하게 유지하는 방향: 각 layer의 연산 시간 = (pixel 개수) x (필터 개수) x (필터당 연산시간)
• 필터의 크기
• 입력 이미지가 큰 경우, (또는 첫번째 계층의 경우) 11x11, 15x15 등 큰 크기의 필터가 이용됨
• 32x32, 28x28 등 이미지의 경우 5x5가 주로 사용됨
• 큰 크기의 필터 1개 사용하는 것보다는 작은 크기의 필터 여러개를 중첩 사용하는 것이 낫다고 함.(즉, 7x7 1개 보다는 3x3 필터 3개 중첩이 낫다고 함): non-linearity에 대한 특징을 좀더 잘 찾아낼 수 있으며, 연산량도 더 적어지기 때문이라고 함.
• 필터의 stride
• convolution 수행 시 건너뛰는 픽셀의 수
• 입력 이미지의 크기가 클 경우, 연산량을 줄이기 위한 목적으로 입력 계층에 가까운 계층에 적용
• 일반적으로는 stride는 1로 둔 뒤, pooling을 통해 subsampling을 거치는 방식의 결과가 낫다고 함.
• zero-padding
• convolution 연산의 경우 경계 처리문제로 인해, 출력되는 feature map의 크기가 입력 이미지보다 작아지게 됨.
• 입력의 경계면에 0을 추가함으로써, convolution 후의 이미지 크기를 입력의 크기와 동일하게 유지할 수 있음.
• 또한 경계면의 정보까지 살릴 수 있음

Papers

• Backpropagation applied to handwritten zip code recognition (LeCun, 1989)
• CNN이 처음 소개된 논문; 필기체 Zip Code 인식을 위한 프로젝트에서 출발.
• Gradient-based learning applied to document recognition (LeCun; Bengio, 1998)
• CNN 구조(LeNet-5)를 설명
• 32x32 필기체 입력 데이터를 10개의 클래스로 분류
• Hierarchical neural networks for image interpretation (Behnke, 2003)
• CNN 개념 일반화
• Best practices for convolutional neural networks applied to visual document analysis (Simard, 2003)
• CNN 개념 확대.
• ImageNet Classification with Deep Convolutional Neural Networks (Krizehvsky; Hinton, 2012)
• AlexNet
• Visualizing and understanding convolutional networks (2013)
• ZF Net
• CNN 특정 구조라기 보다는 (CNN 동작 구조를 이해하기 위한) deconvolution을 이용한 visualization 기법; 즉, CNN 중간 계층에서의 동작이 이미지 공간에서 어떻게 진행되었는지 mapping하여 가시화.
• max-pooling으로 인한 max-location에 대한 switch 정보 유지하여 un-pooling 문제 해결.
• Visualizing 기법 관련 후속 논문
• Return of the Devil in the Details: Delving Deep into Convolutional Nets (Chatfield, 2014)
• deepViz: Visualizing Convolutional Neural Networks for Image Classification (Bruckner, 2015)

Artifacts

ILSVRC 

• ImageNet Large Scale Visual Recognition Challenge
• 이미지 인식 분야 성능 우열을 가리는 대회(2010~)
• image classification의 경우, 1000개 class별로 1000개 입력만 주어지므로 다양한 방식으로 이미지 데이터 개수를 늘리는 방식이 같이 고려됨.
• 3개 분야
• image classification: top-5 에러율(5개 후보 중 하나만 맞으면 맞는 것으로 인정)
• single-object localization: 물체가 존재하는 영역까지 파악. 최대 5개까지의 bounding box에서 ground truth와 50% 이상 영역이 일치하면 맞다고 봄
• object detection: 200 class 학습 데이터를 이용하여, 이미지에 존재하는 object를 가능한 많이 추정하되, false positive에 대해서는 감점을 주는 방식. mean Average Precision(mAP)로 결과를 평가.
• ImageNet: a very large dataset with lots of image categories
• 주요 우승자
• 2012: AlexNet (8 layers)
• 2013: ZF Net, OverFeat (5/6 layer)
• 2014: GoogleNet (22 layers), VGG (19 layers), SPPNet
• 2015: ResNet (152 layers)
• 2016: ResNeXt
• 2017: Xception, Stochastic depth&ResNet (1202 layers), DenseNet

CNN Frameworks (Image Classification)

• LeNet (LeCun)
• LeNet-1 (1990)
• 28x28 입력 이미지, convolution-subsampling-FC 연결 구조, 5x5 filter, max-pooling.
• 3000 free parameters (12만개의 free parameter가 필요한 종래 FC 구조에 비해 훨씬 적은 규모이며, 학습 결과도 낫다고 함)
• LeNet-5
• 32x32 입력이미지, filter 개수 늘어남, FC 크기 커짐.
• 6만 free parameters
• average-pooling
• 'AlexNet' (Krizehvsky; Hinton, 2012) 
• Stride 개념(1단계 계층에서 stride 4를 이용함), Convolution-Convolution 연속 적용
• ReLU, DropOut, overlapped pooling, response normalization, data augmentation
• ReLU: sigmoid 및 tanh 함수에 비해 학습속도 빠르고(6배 정도), back-propagation 결과 단순; non-linear한 성질로 활성화됨; 입력의 normalization 불필요하지만, 출력된 결과를 pooling하기에 앞서서 normalization 필요(response normalization -> 강한 자극이 주변의 약한 자극 전달을 막는 효과; lateral inhibition)
• DropOut: voting 효과 및 co-adaption 회피 효과; FC 계층 처음 2개에만 50% 비율로 적용.
• overlapped pooling: 3x3 window를 stride 2로 사용했음. (일반적으로는 2x2 window를 사용해서 겹치지 않도록 건너뛸 경우, 이미지 크기의 가로/세로 각각 절반씩 총 1/4로 줄어든다.)
• data augmentation: 적은 연산으로 데이터 늘리기. 
• 1) 256x256 원본 이미지에서 10개의 224x224 이미지 부분을 선택; 최종 결과에서는 softmax 출력 평균을 채택.
• 2) 원본 이미지의 컬러 RGB 값에 (PCA를 사용하여) 랜덤변수를 더하여 색상 변화
• GPU
• convolution layer: 전체 연산량의 90~95%, 파라메터 5%, data parallelism(여러 입력 feature map에 동일한 filter 연산 수행)에 적합
• fully connected layer: 연산량의 5~10%, 파라메터 95% (많은 파라메터로 인해 overfitting에 빠지기 쉬움), model parallelism에 적합
• 5개의 convolution, 3개의 FC layers, 중간중간의 max-pooling.
• 224x224x3  컬러이미지를 1000개 클래스로 분류
• 2개의 GPU (GTX580) 적용 고려한 병렬 구조
• 총 5개의 convolution 계층과 3개의 fully-connected 계층으로 구성.
• 65만개 nodes, 60M free parameters, 0.63B connections: 한번 학습하는 데 7일 넘게 소요.

• ‘Network in Network’ (Lin et al. (2013)
• Mlpconv 계층을 제안. 해당 계층 내에서 neuron 간의 복수의 layer를 가질 수 있다는 것을 제시. 
• (CNN의 convolution layer가 local receptive field에서 linear feature를 추출하는 데 우수한 반면,) non-linear feature를 추출하기 위한 방안으로 featuremap 개수를 늘리는 종래 방식 대신, micro neural network을 설계하여, 종래 filter 대신 MLP를 이용한 convolution 방식을 제안함.
• (NIN으로 효과적인 feature 추출이 가능하므로) 최종 계층으로 FC 대신에 Global average pooling을 이용함.
• 1x1 convolution (=1 layer fully-connected neural network)
• 여러 개의 featuremap으로부터 비슷한 성질을 묶어내어, 결과적으로 차원을 줄이는(=연산량을 줄이는) 효과를 제공함.
• ZF Net (2013)
• (Visualizing 기법을 통해,) AlexNet의 hyper-parameter를 수정하여 성능 개선(3% 이상); convolution layer 크기를 확대.
• AlexNet에서는 일부 feature에 몰리거나, aliasing 문제도 발생하는 반면, ZFNet은 필터들에서 다양한 feature가 고르게 나타남.
• 1개의 GPU (GTX580)을 70 epoch, 12일간 학습.
• AlexNet의 첫번째 convolution 계층의 11x11 필터 (stride 4) 대신 7x7 필터 사용(stride 2).
• 필터의 크기가 작고 stride가 작게 설정될 때 결과가 낫다는 것을 확인함.
• 2개의 GPU에 인위적으로 다른 처리를 하는 시도가 불필요함을 보임.
• layer 별로 feature 습득 시간이 다름을 확인.
• 앞쪽 layer가 몇번의 epoch에 feature가 수렴되는 반면, 뒤쪽 layer는 40~50 epoch이 되어야 feature가 보이기 시작.
• 뒤쪽 layer로 갈수록 이미지 크기/위치변화/회전변화에 invariance 확보.
• 개체의 정확한 위치까지도 파악 가능.
• GoogLeNet (Szegedy, 2014)
• (AlexNet에 비해 전체 망의 깊이는 깊어졌지만) Inception Module 개념 도입을 통해 전체 free parameter 수 감소(1/12) 가능: 9개의 인셉션 모듈 사용.
• AlexNet: 60M -> GoogLeNet: 5M 
• (Inception: 남에게 어떤 생각을 주입하거나 생각을 읽어내는 개념을 차용하여), DNN을 이용하여 데이터로부터 중요한 정보를 얻어내는 것에 연상된 이름으로 판단됨.
• 동일 layer에 서로 다른 크기를 가진 convolution filter를 적용; 1x1 convolution을 이용하여, 차원을 줄였기(dimensionality reduction) 때문에 가능한 구조. (참고)

• auxiliary classifier (=SuperVision)
• 망이 깊어지면 vanishing gradient 이슈로 인해 학습 속도 저하 및 overfitting 문제가 발생한다. 
• Re-LU 활성함수이용시, (sigmoid 또는 cross-entropy보다는 낫지만) 여전히 작은 값들이 곱해지다 보면 0 근처로 수렴되는 상황이 나올 수 있음.
• 학습을 위한 도우미로서 'reguarizer'와 같은 역할; auxiliary classifier가 batch-normalize되었거나 drop-out layer를 가질 경우, 최종 계층의 classifier 결과가 향상된다고 함.
• factorizing convolutions
• 커다란 크기의 filter(=convolution kernel)를 여러 계층의 작은 크기 filter로 대체하여 연산량 절감 가능.
• 5x5 convolution을 2단의 3x3 convolution으로 구현할 경우 25개의 free parameter를 18개로 대체하므로 28%의 연산 절감이 가능하다고 함; 같은 방식으로 7x7을 3단의 3x3으로 구현시 49 -> 27 (45% 절감).
• 3x3을 1x3과 3x1로 분해할 경우, 9 -> 6 (33% w절감).
• Testing
• 하나의 테스트 이미지(256x256)를 4개 크기로 변화시킨 뒤, 3개씩의 정사각형 부분을 선택하여, 6장의 224x224 크기를 선택하여 좌우반전 --> 4x3x6x2 = 144개의 이미지 생성하여 voting 결과를 이용.
• VGGNet (Simonyan, 2014)
• Oxford
• 3x3 convolution, 2x2 max pooling 으로 구성된 (GoogLeNet 보다) 단순한 구조
• (AlexNet에서의 커다란 필터를 사용하는 대신) 균일한 크기의 3x3 filter로만 receptive field를 설정함.
• depth가 성능에 어떤 영향을 주는 지 확인하기 위한 6개의 구조를 살펴본 결과 (ILSVRC-2012 데이터의 경우에는) depth 16에서 최적의 결과가 나오는 것을 확인
• 메모리와 파라미터 개수(133M ~ 144M)가 많이 필요하다는 것(그리고, GoogLeNet의 3배 연산량 소요)이 단점; 대부분의 파라미터(122M)는 FC 계층 3개에서 발생함.

• 이슈
• Local Response Normalization(LRN)이 별 효과가 나타나지 않았다고 함.
• 1x1 convolution이 적용되기는 하지만, 차원을 축소하기 위한 목적보다는, 차원을 그대로 유지하면서, ReLU를 통해 추가적인 non-linearity를 확보하려는 목적.
• vanishing/exploding gradient 문제를 해결하기 위해, 구조A(11개 계층)의 학습 결과(특히, 앞의 4개 계층과 마지막 FC 계층)를 pre-training 모델로서 보다 깊은 계층을 가진 구조의 parameter 초기값 설정에 이용함.
• (다양한 크기의 이미지에 대응할 수 있도록) 학습 입력 이미지의 scale을 무작위로 변화한 뒤(scale jittering) 무작위로 224x224를 선택; 
• 테스트 데이터에 대한 multi-crop data augmentation(1장 -> 150장) 기법과 dense evaluation 개념을 함께 적용하여 성능 개선 시도.
• 관련 논문
• Deep inside convolutional networks: Visualising image classification models and saliency maps (Simonyan, 2013)
• Understanding Deep Image Representations by Inverting Them (Mahendran, 2015)
• ResNet (He, 2015)
• Deep residual learning for image recognition (He, 2015)
• DNN의 계층이 adding 됨에따라(=network depth가 깊어질수록) 성능이 저하되는 현상에 대한 대응. -> x와 H(x) 간의 관계를 학습하기 보다는, x와 H(x)의 차이(residual)를 학습하도록.
• residual framework
• 깊어진 망에서도 쉽게 최적화가 가능함; 늘어난 깊이로 인해 정확도가 개선됨
• CNN의 depth를 100개 이상 깊게 늘리면서도 학습 효율을 떨어뜨리지 않는 방안 고민의 결과
• residual learning: 입력의 작은 움직임(residual)을 학습한다는 관점
• 몇 개의 layer를 건너 뛰면서, 입력과 출력이 연결(shortcut)되는 구조이므로 (파라미터가 늘어나는 것도 아니면서) 연산량 증가가 미미하면서도, forward/backward path가 단순해지는 효과.
• 152 layers, Top-5 오차율 3.57%
• classification, localization, detection 분야 모두 우승.
• GoogLeNet (오차율 6.7%)보다 성능 2배 개선
• 특징
• VGG Net 설계 구조 활용: 대부분 3x3 convolutional kernel 이용. 복잡도(연산량)를 줄이기 위해, max-pooling, FC, dropout을 최대한 배제함
• Feature map 크기가 절반으로 작아지는 경우, 연산량의 균형을 맞추기 위해 필터의 수를 2배로 늘림; Feature map 크기를 줄이기 위해서는 (pooling을 사용하는 대신) convolution에서의 stride 크기를 2로 취함.
• 2개의 convolution layer마다 shortcut connection 연결.
• 학습 초기 단계에서 residual net의 수렴 속도가 plain network 보다 빠름.
• 최종 결과 제출시 2개의 152 layer 결과를 조합한(또는 depth를 서로 달리하는 6개 모델을 이용한) ensemble 결과를 제출했다고 함.
• CIFAR-10에 대한 110/1202 계층에 대한 실험을 통해, 천 개 이상의 계층이 구성될 경우에도 어느 정도의 성능이 나오지만, 망의 깊이를 고려한 데이터 양의 부족으로 인한 overfitting 발생이 된 것으로 판단됨 --> Identity mappings in deep residual networks (He, 2016)에서 pre-activation 기법(=activation을 short-cut connection 앞쪽에 배치하여 regularization 효과 높임)을 통한 개선된 ResNet 방안 제시됨; identity skip connection (shorcut connection에 어떠한 변형도 가하지 않은 경우) 속도나 성능이 최적임을 확인.
• Faster R-CNN의 개념이 ResNet으로 다시 이어진다고 간주됨.
• bottleneck architecture
• 2단의 3x3 convolution 계층을 1x1 - 3x3 - 1x1 세 개의 계층(병목 형태 구조)로 변경하여, 연산량(연산시간)을 절감
• 참고: Deep Residual Networks with 1K Layers 
• 1000 계층 pre-trained model 오픈소스 (Torch 기반)
• Google Inception
• 연산 비용을 늘리지 않으면서도 NN을 scale up 할 수 있는 방안을 탐구
• Rethinking the inception architecture for computer vision (Szegedy, 2015)
• inception 모듈 내에 convolution (최종 계층의 stride 2) 및 pooling (stride 2)을 나란히 배치한 뒤 concat하여, 효율성과 연산량을 절감. -> 학습모델스스로 어떤 convolution/pooling을 하는 게 좋은 결과가 나오는 지를 결정할 수 있도록 하자. 이때, 연산량이 늘어나는 문제를 해결하기 위해 1x1 convolution 적용해보자.
• 즉, 단순하게 pooling layer를 적용하는 것보다, convolution layer와 나란히 적용하는 게 효과적이라는 것을 확인
• Inception-V2 (2015)
• 42개 layer.
• Inception-V1에 BN(batch normalization)을 반영한 기본 모델.
• 'BN-Inception'
• 299x299x3 입력 지원; (종래 7x7 convolution을) 3단의 3x3 convolution으로 대체 및 convolution kernel 인수분해 방식 적용.
• batch-normalized auxiliary classifier 적용시 regularization 효과 극대화.
• Inception-V3
• 144개 multi-crop 데이터 적용.
• Inception-V2에 convolution factorization, label smoothing, auxiliary classifier, BN을 결합시킨 모델
• Inception-V4
• Inception-v4, Inception-ResNet and the Impact of Residual Connections on Learning (Szegedy, 2016)
• Stem (9 layers): 299x299x3 입력 이미지를 35x35x384의 feature map로 생성.
• 3가지 형태의 inception 모듈 (A, B, C), 2가지 형태의 reduction 모듈 사용.
• Inception-ResNet
• Inception 구조에 ResNet 개념 접목을 통해 ResNet 보다 성능이 좋다는 것을 보임; Inception-V3보다 학습속도도 빠름(=훨씬 적은 epoch에서 최적 성능 나타나기 시작)
• V1, V2: Stem에 적용된 layer 구조가 다름 (즉, V1의 stem은 단순 구조, V2의 stem은 inception-V4와 동일); ResNet-V2의 필터 개수가 더 많음.
• ResNet의 residual connection 구조에 1x1 convoluton을 적용하여 일부 변경.
• Inception-V4와 3개의 Inception-ResNet-V2 ensemble을 했을 때, Top-5 error 3.1%라고 함.
• ResNeXt
• Aggregated Residual Transformations for Deep Neural Networks (Xie; Girshick; He, 2017)
• convolution 빌딩 블록의 개수(=cardinality)를 늘려서 분류 정확도를 향상.
• depth 또는 channel 수를 늘리는 것보다 cardinality를 키우는 것이 낫다는 결과.
• bottlenet block에서 그룹별 convolution 구조를 이용하여 sparse한 연결이 이루어 질 수 있도록 했다고 함.
• Xeption
• extreme inception
• spation correlation (= width x height과 cross-channel correlation (=depth)을 독립적으로 다루도록 함. -> 즉, 종전방식 처럼 한번에 depth를 묶어서 보는 대신, 크기에 대한 convolution 먼저 한 뒤, depth convolution을 수행하는 방식을 제안.
• depthwiase separable convolution = depthwise convolution + pointwise convolution (=1x1 cross-channel convolution)
• DenseNet
• Densely Connected Convolutional Networks (Huang, 2016)
• 즉, layer가 순차적으로 연결될 뿐만 아니라 건너뛰면서 연결될 수 있도록 함.
• ResNet의 영향 및 stochastic depth 개념(저자의 다른 논문; ResNet을 1202계층까지 쌓았음)에서 영향을 받았음; 

Object detection

• 배경
• 물체를 인식하기 위해서는 'feature extraction'과 'object classifier' 두 가지 기능이 갖추어져야 함.
• feature 추출: 종래에는 gradient 기반 vision 알고리즘(SIFT, HOG) 이용됨
• object 검출: SVM, DPM 이용됨.
• Regions with CNN features(=R-CNN) 
• Rich feature hierarchies for accurate object detection and semantic segmentation (Girshick, 2014)
• 버클리. 
• (AlexNet, 2012) classification 결과를 참고하여, detection 분야에 CNN 적용
• 종래 이미지 low-level gradient 속성에 대한 인식 알고리즘(SIFT, HOG)에 비해 좋은 결과 도출.
• 입력 데이터로부터 2000개의 후보 영역(region proposal)을 생성(Selective Search) 한 뒤, warping(늘리기)/crop(잘라내기)을 사용하여 224x224 크기로 변형하여 CNN에 입력 후 CNN feature vector를 얻어냄; 이후 linear SVM fitting을 이용하여 해당 영역을 분류(bounding box regressor)함
• Selective Search (Uijlings, 2013): segmentation의 장점과 exhaustive search 장점을 골고루 활용 (즉, segmentation을 통해 후보 영역의 seed를 설정한 뒤, 이를 기준으로 exhaustive search를 수행) ; 단순 정보(색상, texture) 뿐 아니라 내재된 계층 구조까지 활용하는 기법 (즉, 영상이 표현하고 있는 계층 구조를 통해 크기에 상관없이 대상을 찾아냄); 더불어 다양한 컬러 공간(RGB -> HSV[색상,채도,명도]) 이용; 개체 detection을 위한 후보 영역 검출을 위해 2013~2015 주목을 받다가, Faster R-CNN 등장 이후 인기가 감소함.
• Efficient Graph-Based Image Segmentation (Felzenszwalb, 2004): 의미있는 부분으로 효율적인 segmentation 수행; grid graph weighting, nearest neighbor graph weighting 제시.
• ILSVRC 데이터를 이용하여 CNN pre-training을 통해 파라미터 초기화한 뒤, PASCAL VOC(Visual Object Class)를 이용하여 fine tune 수행.
• detection 성능을 58%까지 끌어올림.
• 문제점
• 이미지 크기를 224x224 크기로 맞추기 위해 이미지 변형 및 손실이 발생하여 성능 저하 요인 존재.
• 2000개의 region proposal에 대한 순차적인 CNN 수행으로 인해, 학습 및 실행 시간이 많이 소요. --> 성능은 뛰어나나 속도가 느림; PASCAL VOC07 데이터 5천장 학습에 2.5일 소요 및 수백GB 저장 공간 요구; K40 GPU 이용했을 경우, Object detection 1장 수행에 47초 소요.
• region proposal, SVM 튜닝 등이 GPU 사용에 적합하지 않음
• 후속 연구로 Fast R-CNN (Girshick, 2015), Faster R-CNN (Ren; He; Girshick, 2015) 발표됨.
• Spatial Pyramid Pooling in Deep Convolutional Networks for Visual Recognition (=SPPNet) (He, 2014)
• AlexNet 구조에서, convolution layer는 sliding window로 인해 입력 크기에 영향을 받지 않으며, FC layer가 큰 영향을 받는다는 점에 주목.
• 입력 이미지를 crop/warp 하는 대신에, convolution의 결과를 spatial pyramid pooling을 수행하여 FC layer에 전달하는 방식을 이용; 즉, spatial bin으로 불리는 M개의 영역을 피라미드 방식으로 계산한 결과를 concatenation 시킨 뒤, 사전에 설정된 크기로 FC에 전달.
• Bag of Words (BoW) 개념: 특정 개체를 분류하는 있어, 굵고 강한 특징에 의존하는 대신, 여러개의 작은 특징을 사용하여 개체를 구별.
• 오직 1번만 convolution 과정을 거친 뒤, 피라미드 방식의 pooling을 수행하기 때문에, R-CNN에 비해 (학습 3배 빠르고, 실제 적용시는) 10~100배 빠른 성능을 보인다.
• Fast R-CNN (Girshick, 2015)
• 목표
• 검출 정확도(mAP)가 R-CNN/SPP Net보다 좋을 것; single-stage 학습 수행; 학습 결과를 모든 layer에 업데이트; feature caching을 위한 별도 저장 공간 불필요하도록.
• 특징
• 입력 이미지에 대한 ConvNet 연산 1회 수행을 통해 RoI pooling 계층(=Single-level pooling)에서 후보 영역을 뽑아낸 뒤 FC계층에 넣음.
• R-CNN/SPP Net에서 mini-batch를 128개(128장 이미지에서 하나씩 128개 RoI를 선택 = resion-wise sampling)로 수행했었으나, (원본 입력 이미지 크기에 대한 scale 처리를 따로 하지않는) Fast R-CNN에서는 hierarchical sampling 기법을 통해 2장의 이미지로부터 64개의 샘플을 뽑아 128개의 RoI를 정하도록 설정. --> 학습 과정에서 학습 결과를 공유할 수 있게되어 연산 속도가 빨라진다고 함.
• (PASCAL VOL 이미지 데이터에 대한) detection 성능이 70% 수준 근처까지 올라왔다고 함.
• 다음의 그림에서처럼, 출력부분의 softmax는 class를 구별하고, bbox regressor는 개체의 위치 정보를 구하는 역할을 수행한다.

• Faster R-CNN
• Faster R-CNN: Towards real-time object detection with region proposal networks (Ren; He; Girshick, 2015)
• 목적:
• Fast R-CNN이 종래 R-CNN에 비해, 이미지 처리 속도를 크게 향상시켰으나, test time에 (region proposal 고려시) 2초가 걸리는 것을 더욱 개선할 필요가 있음.
• (Region proposal을 위한 별도 과정을 거치는 대신에,) ConvNet에 region proposal을 위한 특수 용도의 네트워크(RPN)을 추가하였음; 즉, RPN에서 object가 있을만한 영역에 대한 proposal을 생성함.
• 특징
• Region proposal network: conv feature map에 대한 각각의 sliding window에서 scale과 aspect ratio를 달리하는 조합(=anchor)를 구하여 k개의 후보 영역을 지정하여 256/512 차원의 벡터 정보로 전달.
• 종래 Selective Search, Edge Box 방식의 후보영역 선택 방식에 비해 성능 개선이 가능하다고 함: 즉, VGG 프레임워크 기준으로, SS + Fast R-CNN에 약 2초가 소요된 반면, RPN + Fast R-CNN은 0.2초가 소요됨.
• 이후, Faster R-CNN의 기법은 ResNet이 object detection으로 적용됨에 있어 더욱 발전적으로 활용된다고 함.
• Network on Conv feature map (=NoC)
• Object Detection Networks on Convolutional Feature Maps (Ren; He; Girshick, 2016)
• CNN을 이용한 feature 추출 방법이 종래 computer vision 알고리즘에 비해 성능이 우수하다는 점을 이용하여, ResNet으로 구현 적용; Region proposal  및 RoI pooling 부분 역시 ConvNet으로 구현 가능.
• object classifier에 대한 부분을 NoC라고 명명하고, 어떻게 구현해야 최적의 성능이 나올 수 있는 지 실험을 통해 확인; FC 2~3개 만을 이용하는 종래 방식에 비해, Conv를 거쳐 maxout를 결합한 방식이 FC 앞쪽에서 들어올 경우 결과 개선이 가능하다는 것을 확인
• 특징
• ResNet의 Conv 계층 앞부분을 feature extractor로 활용하고, Conv 계층 후반부 및 Classifier를 Fast R-CNN 구조로 변형하고 구현함으로써, VGG-16(73.2%)을 사용했을 때보다 정확도 개선(76.4%). 

• Mask R-CNN
• ResNeXt를 활용.
• RoIAlign 방식으로 후보영역 추출
• 클래스별 마스크 분리

single-object localization

• OverFeat
• OverFeat: Integrated Recognition, Localization and Detection using Convolutional Networks (Sermanet, LeCun, 2013)
• Testing
• multi-crop voting 방식(서로 겹치는 부분이 있더라도 ConvNet 연산을 전부 새롭게 해야함) 대신 dense evaluation 방식 이용.
• offset을 오밀조밀하게 구성한 non-overlapped pooling을 통해, resolution이 낮아지는 문제를 해결.
• 1-pass로 연산 가능한 구조
• 이후 등장한 SPP Net역시 1-pass 구조를 취하고 있으며, OverFeat의 성능과 속도에 크게 앞선 결과를 도출하였음.
• FC layer에 대한 해석 (by LeCun, 2015)
• = convolution layer with 1x1 convolution kernel and a full connection table = "fully connected layers" really act as 1x1 convolutions = ConvNets에 굳이 fixed-sized input이 요구될 필요가 없음
• 즉, FC 계층에 들어가는 feature map의 크기를 고정시키기 위한 노력이 불필요하다고 해석함. 따라서, 입력 이미지의 크기가 다를 경우, slide를 조절하여, 일정한 resolution으로 크기가 들어오도록 조절 가능하고, voting을 통해 판단함.

Python Application

• Think DSP
• Digital Signal Processing in Python, by Allen B. Downey.
• https://github.com/AllenDowney/ThinkDSP
• Python으로 신호 처리, 음악의 스펙트럼을 조정하는 예시.

• 주피터 노트북으로 그래프 그리기
• https://nbviewer.jupyter.org/github/mircealex/Movie_ratings_2016_17/blob/master/Mv_ratings_project.ipynb

Confusion Matrix, Sensitivity, Specificity

Cohen's kappa

• the kappa as a measure of agreement between 2 individuals 
• 2명의 평가자가 평가한 분류 결과가 얼마나 일치하는 지에 대한 통계적 지표
• 친절한 한글 설명(2012.01)
• 상세한 영문 설명(2014.01)
• the kappa statistic is a measure of how closely the instances classified by the machine learning classifier matched the data labeled as ground truth
• Kappa = (observed accuracy - expected accuracy)/(1 - expected accuracy)
• 대략 0.75 이상이면 훌륭하고, 0.4 이상만 되도 우수하다고 볼 수 있다고 함.
• Kappa is an important measure of classifier performance, especially on imbalanced data set.
• it measures how much better the classier is comparing with guessing with the target distribution.
• 데이터 집합이 밸런스가 맞지 않을 경우, 대충 찍어서 맞추어도 성능(정확도)이 좋은 것으로 나오는 상황에 대한 대응을 하는 차원에서의 평가지표로 이용된다고 볼 수 있음.

Case Study

특정 이벤트를 Positive class로 전제할 때, ...

• 서비스 도메인의 특징: (이벤트 신호를 놓치더라도 다시 이벤트 신호를 살펴볼 기회가 있는 상황에서는) 실제 정상 신호를 이벤트라고 판단하는 것(FPR, 거짓긍정률)을 막는 게 양치기 소년 효과를 막기 위해서 더 중요함. 따라서, 현실적으로는 Specificity (참 부정률)이 높아져야 함. 즉, 실제 정상이면 정상이라고 판단해야지, 이벤트로 오판하면 시스템 전체의 신뢰도가 무너질 수 있음.

• 물론, 이론적으로는 실제 이벤트를 이벤트라고 판단(리콜=민감도=참 긍정률)하고, 이베트라고 예측했을 때 이벤트가 정말 맞을 확률(정밀도)가 높은게 이벤트를 잘 맞춘다는 평가치(=F1 기준)가 될 것임.
• 참 긍정률 TPR = Sensitivity(민감도) = Recall(재현율) ; 실제 이벤트를 얼마나 잘 구별했나? (실제의 전체 이벤트 중에서 이벤트가 일어났음을 정확히 판단할 확률)
• 참 부정률 TNR = Specificity(특이도) ; Normal을 얼마나 잘 구별했나? (실제 전체의 정상 신호 중에서 정상이라고 정확히 판단할 확률)
• 예시: 어떤 검사방법의 적합성을 평가하는 방법으로 민감성과 특이성의 개념을 사용할 때,
• 민감성이란 (전체 질병을 가진 사람 중에서, 실제) 질병이 있는 사람을 양성(질병이 있다고)으로 검출하는 능력. 즉 A/(A+B) 
• 특이성이란 (전체 질병이 없는 사람 중에서, 실제) 질병이 없는 사람을 음성(질병이 없다고)으로 검출하는 능력. 즉 Y/(X+Y)
• Kappa ; 우연에 의하지 않은 관찰된 일치율 / 우연에 의하지 않은 최대 일치율 ;  0.8 이상이면 좋다고 함.
• F-Score: Precision과 Recall의 조화평균 = 2*(Precision*Recall)/(Precision+Recall)
• 정확도 Accuracy ; 전체 데이터 중에서 정확히 맞춘 것만 따지기.
• 정밀도 Precision ; 이벤트라고 예측된 것 중에 진짜 이벤트가 들어있을 확률
• Precision과 Recall을 재미있게 설명한 블로그 (2016.06)
• 전체 선물로 받은 것 중에서 정확히 기억한 것의 비율 = recall = sensitivity
• (실제로는 10개를 선물 받았었는데) 무언가 기억해낸 5개 중에서, 3개가 정확할 경우의 recall = 3/10 = 30%
• --> 전체 10개 중에서 몇 개나 기억해냈는가
• 기억해 낸 것 중에서 정확하게 기억해 낸 것의 비율 = precision 
• (실제로는 10개를 선물 받았었는데) 무언가 기억해낸 5개 중에서, 3개가 정확할 경우의 precision = 3/5 = 60%
• 이 때의 5개는 선물 받았다고 추정해 낸 Postive 추정값.
• --> 내가 기억해 낸(예측한) 정밀도가 어떠한가

Latex, Lyx, TexLive

개요

• 기존 윈도우에서 잘 사용하던 Lyx 환경을 새로운 윈도우 환경으로 옮기면서, MikTeX 패키지 설정에 어려움이 많던차에, 한글도 지원된다고 하는 TexLive로 옮겨타기로 했다.

비교

• MikTeX
• 윈도우 전용; 최소한의 패키지
• TexLive
• 한글 지원; 윈도우/맥/리눅스

설치 개요

• 윈도우 10
• TexLive 2016 다운로드 받아서 설치
• http://tug.org/texlive/
• 패키지 설치 시간 고려하면 상당히 시간 걸림
• 설치파일(intall-tl-windows.exe) 실행시 관리자 권한으로 실행
• (Install Full) 기본은 full scheme 설정하는 방식: ~3383개
• 잘 설정할 자신이 있다면 small scheme 선택: ~2241개
• 참고 블로그: http://woogyun.tistory.com/533
• Path 설정
• TeX의 실행파일 폴더(예: D:\texlive\2016\bin\win32)를 추가
• 기본 에디터 또는 별도 TeX 편집기 (TeXstudio 또는 Lyx) 설치
• TexLive 기본 에디터는 TeXworks 
• 예를 들면, 기본 notepad 수준
• http://www.texstudio.org/
• 예를 들면, 워드 수준
• https://www.lyx.org/
• 예를 들면, 노트패드++ 수준
• 이외, Texmaker 또는 온라인 LaTeX
• 참고 블로그: http://t-robotics.blogspot.kr/2016/02/latex.html
• TeX 에디터 종류: https://en.wikipedia.org/wiki/Comparison_of_TeX_editors

Sample.tex

• https://gist.github.com/chkwon/821ee403b67aa46ee166
• or use the following;

% -*- coding: utf-8 -*-
\documentclass{oblivoir}
\usepackage{kotex}
\title{처음 만든 \LaTeX\ 문서}
\author{고길동}
\begin{document}
\maketitle
처음 만든 \LaTeX\ 문서입니다. 한글을 사용하려면 \verb|\usepackage{kotex}|을 사용해야 합니다.
\end{document}

 Figure

• 가급적 벡터 이미지를 사용하기: eps, pdf
• 일러스트, 파워포인트, Inkscape
• 불가피한 비트맵 이미지: png, tiff

Usage Tips

• 참고 블로그: 
• http://stom.chkwon.net/latex/
• http://formal.korea.ac.kr/~jlee/lectures/cnce150/
• .bib 파일은 JabRef을 통해서 관리
• 최종 PDF 출력에는 pdflatex과 PDF image formats이 가장 적당하다고 함.
• 편집 > 환경 설정 > 문서 처리 > 문서 처리 도구 기본값
• 한글 사용하려면 다음과 같이
• \usepackage{kotex}

윈도우 10 단축키

• 윈도 + Tab : Task bar
• 윈도 + Ctrl + D : 가상 데스크톱 만들기
• 윈도 + Ctrl + F4 : 가상 데스크톱 닫기
• 윈도 + Ctrl + 좌우 방향키 : 가상 데스크톱 이동
• 윈도 + A : Action Center
• 윈도 + I: 설정화면
• 윈도 + S : Search
• 윈도 + K : 무선 장치
• 윈도 + 좌우방향키 : 선택 창 정렬
• 윈도 + Shift + 좌우방향키 : 외부 화면 연결시 선택 창을 이동
• 윈도 + P : 외부 화면 연결

Ubuntu 16.04 한글 입력 설정

한글 설치

• 16.04에서는 IBus가 한글 입력을 기본으로 제공하지 않기 때문에, Fcitx를 사용하는 게 낫다. 또한 시스템 언어 설정에서 한글 언어를 사용한다고 설정하면, fcitx-hangul이 설치된다. 
• $ sudo apt-get install fcitx-hangul
• 따라서 언어 설정에서, Keyboard input method system을 ibus가 아닌 fcitx로 변경하면 된다.
• 상단 메뉴바 오른쪽 입력기에 키보드 표시가 fcitx 아이콘임

한글 키보드 입력 및 한영 전환

• 참고 블로그
• http://hochulshin.com/ubuntu-1604-hangul/

• AllSettings > Keyboard > Shortcuts Tab > Typing 선택 후
• 설정되어 있는 Key들을 (backspace 눌러서) 모두 Disabled로 변경 
• Compose Key를 Right All로 선택
• Switch to next source는 한영키를 눌러 Multikey로 선택
• fcitx아이콘을 눌러서 Configure Current Input Method를 선택
• Keyboard-English(US)가 있다면 +를 눌러 Hangul을 추가
• Global Config tab에서 Trigger Input Method는 한/영키를 눌러 Multikey로 설정(왼쪽 오른쪽 모두)
• Extrakey for trigger input method는 Disabled로 설정
• Global Config tab에서 Program > Share State Among Window > All을 선택

XPS 15 9560 Dual Booting

부팅 USB 스틱 만들기

• 우분투에서 부팅용 USB 만들기
• http://pinkwink.kr/871
• $ sudo apt install unetbootin

멀티 부팅

• XPS 13에서 윈도우 10과 우분투 16.04 멀티부팅하기
• http://pinkwink.kr/998
• F12 또는 F2로 Bios 셋업
• 1) System Configuration / SATA Operation
• RAID On을 AHCI로 변경
• 2) Secure Boot / Secure Boot Enable
• Enabled에서 Disabled로 변경
• 3) General / Advanced Boot Option
• Enabled Legacy Option ROMs를 check

• 우분투 설치를 위해 윈도우10에서 사전에 해 주어야 할 작업
• System Settings에서 Fast Startup를 멈추어 주기
• https://www.tenforums.com/tutorials/4189-fast-startup-turn-off-windows-10-a.html
• 기존 윈도우 설치된 파티션의 크기를 축소
• 나중에 우분투 설치시 
• swap: 32 x 1024 = 32,768 MB
• ext4 / 충분히

• SATA Operation
• RAID is the right setting for Windows anyways. AHCI is only required if the OS don't has Intel RST drivers, like Linux. 
• f you installed Windows in RAID mode (which is not technically RAID but Intel RST) you can't switch to AHCI later, Windows will no longer properly boot. Also RST is the "correct" mode anyway to get the maximum speed and power savings.

• 윈도우 10 듀얼 부팅 모드로 설치된 우분투를 제거하는 방법 (UEFI 기준)

• grub 오류로 인한 멀티부팅 복구 방법
• http://pinkwink.kr/868
• boot-repair
• 윈도우 부팅이 안될 경우,
• Intel RST driver가 없으면 PCie SSD를 인식하지 못함
• CPU가 스카이레이크 Win 10일 경우, UEFI boot ; Security Off

• grub 조정 방법
• https://www.howtogeek.com/howto/43471/how-to-configure-the-linux-grub2-boot-menu-the-easy-way/
• $ sudo add-apt-repository ppa:danielrichter2007/grub-customizer
• $ sudo apt-get update
• $ sudo apt-get install grub-customizer

Python, Jupyter

NumPy, SciPy, Pandas, and Matplotlib are fundamental scientific computing and visualization packages with Python.

• 참고 블로그:
• http://freeprog.tistory.com/63
• http://webnautes.tistory.com/799
• http://blog.danggun.net/4069
• https://machinelearningmastery.com/setup-python-environment-machine-learning-deep-learning-anaconda/

• 설치 방법1 : pip를 이용해서 설치하는 방식 
• $ sudo apt-get update
• $ sudo apt-get install python-pip
• $ pip list
• $ sudo pip install -U numpy
• (만약 필요하다면 다음을 먼저 수행) 
• $ sudo apt-get install python-dev
• $ sudo apt-get install libblas-dev liblapack-dev
• $ sudo pip install -U scipy
• (만약 필요하다면 다음을 먼저 수행) 
• $ sudo apt-get install gfortran
• $ sudo apt-get install libpng-dev libfreetype6-dev libjpeg8-dev
• $ sudo pip install matplotlib
• $ sudo pip install -U scikit-learn
• $ sudo pip install jupyter
• (만약 설치후 jupyter가 실행되지 않는다면 다음과 같이 해보기)
• $ ~/.local/bin/jupyter-notebook
• 상기 명령이 먹힌다면, ~/.bashrc 에 다음 문장 넣어서 구동하기 export PATH=$PATH:~/.local/bin
• 그런데, 지금까지 주욱 잘 설치가 되도, 막상 jupyter 구동하면, kernel 찾을 수 없다는 메시지 나올 수 있음
• 설치 방법2: anaconda3을 이용해서 쉽게 설치
• 참고 사이트
• 윈도우 기준 설명: http://agiantmind.tistory.com/172
• https://ipython.readthedocs.io/en/latest/install/kernel_install.html
• 다음의 사이트에서 원하는 버전의 python installer 선택하여 다운로드
• https://www.continuum.io/downloads
• $ bash Anaconda3-4.3.1-Linux-x86_64.sh
• 기본적으로 /home/user/anaconda3 에 설치된다.
• 기본적인 conda 명령들
• 참고: https://conda.io/docs/test-drive.html
• $ conda update --help
• $ conda --version
• $ conda update conda
• $ conda info --envs
• $ conda list
• exercise
• $ conda create --name eclc python=3.5 ipykernel
• $ conda install --name eclc numpy pandas matplotlib scipy pip
• (예제 패키지) https://docs.continuum.io/anaconda/pkg-docs
• $ conda info --envs
• $ source activate eclc
• $ python -m ipykernel install --user --name eclc --display-name "Python3.5 (eclc)"
• $ source deactivate
• $ conda remove --name eclc --all
• $ jupyter notebook
• packages
• pip install 대신에 conda install 을 사용할 것.
• pip는 anaconda 패키지 위치에 설치되는 것이 아니라 기본 System 패키지 설치 위치에 설치됨
• 필요한 경우, conda install로 pip를 설치한 뒤, 해당 env에서 pip로 설치
• $ conda install -n eclc pip
• $ source activate eclc
• $ pip install emcee corner

• 기타
• virtualenv가 필요한 경우
• sudo pip install virtualenv
• pip list 구동시 ImportError 나올 때
• $ sudo apt-get purge -y python-pip
• $ wget https://bootstrap.pypa.io/get-pip.py
• $ sudo python ./get-pip.py
• $ sudo apt-get install python-pip
• Jupyter 다중 kernel 설정
• $ jupyter kernelspec list
• pytorch 설치 방법
• $ conda install pytorch torchvision cuda80 -c soumith
• Checking versions

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25

# scipy import scipy print('scipy: %s' % scipy.__version__) # numpy import numpy print('numpy: %s' % numpy.__version__) # matplotlib import matplotlib print('matplotlib: %s' % matplotlib.__version__) # pandas import pandas print('pandas: %s' % pandas.__version__) # statsmodels import statsmodels print('statsmodels: %s' % statsmodels.__version__) # scikit-learn import sklearn print('sklearn: %s' % sklearn.__version__) # tensorflow import tensorflow print('tensorflow: %s' % tensorflow.__version__) # keras import keras print('keras: %s' % keras.__version__)

cs

• Tensorflow 설치하기
• 참고사이트: 
• https://www.tensorflow.org/install/install_linux
• https://www.tensorflow.org/install/install_linux#the_url_of_the_tensorflow_python_package
• $ source activate eclc
• $ pip install --ignore-installed --upgrade  https://storage.googleapis.com/tensorflow/linux/cpu/tensorflow-1.0.1-cp35-cp35m-linux_x86_64.whl
• GPU 기반으로 설치하기 위한 노력:
• http://luke77.tistory.com/44
• 만약 pycharm 등 외부 IDE에서 tensorflow가 import 되지 않는다면, Settings>Project Interpreter 설정을 anaconda3/envs 아래의 적정한 python 실행기로 변경 설정하면 됨.

• Jupyter, Python
• Reproducible Data Analysis in Jupyter: 
• https://jakevdp.github.io/blog/2017/03/03/reproducible-data-analysis-in-jupyter/?imm_mid=0ef31d&cmp=em-data-na-na-newsltr_20170322
• Jupyter와 python을 이용하는 친절한 데이터 분석 튜토리얼 & 동영상.
• Jupyter Notebook Tutorial: The Definitive Guide
• https://www.datacamp.com/community/tutorials/tutorial-jupyter-notebook
• Jupyter resources
• 나름 유명한 예제들
• Python Quickstart
• http://jorditorres.org/teaching-activity/hands-on-1-python-quick-start/
• Free python books
• https://pythontips.com/2014/02/04/free-python-books
• Python 추천 도서
• Python Essential Reference (David Beazley, 2009, 4판): (2017년 5판 작업 시작). 처음 200페이지 정도가 핵심. 뒤쪽 500페이지는 레퍼런스.
• Fluent Python (Luciano Ramalho, 2015): 효율적인 개념 이해.
• Python Cookbook: 2판은 개념 설명, 3판(2013)은 python 3.3에 집중.
• Python 기반 병렬 프로그래밍 설명 블로그
• Numpy tutorial (Stanford)

Parametric, Clustering, GMM, EM, kNN

https://wikidocs.net/7679

Parametric / Non-parametric Machine Learning

• 참조: 
• http://machinelearningmastery.com/parametric-and-nonparametric-machine-learning-algorithms/
•  Gareth, Introduction to Stat. Learning, 2013
• Parametric (모수적)
• ML 알고리즘은 기본적으로 학습 데이터로부터 매핑 함수를 학습하는 것임. 이 때, 학습 절차를 단순화하기 위해 여러 가정(assumption)이 전제될 경우가 있을 때(예를 들어, 고정된 숫자의 파라메터로 요약한다던가).
• 로지스틱 회귀, LDA, Perceptron, Naïve Bayes
• 이해하기 쉽고, 학습속도 빠르고, 적은 데이터로도 fit 가능.
• 특정 형식으로 모델이 제한되고, 단순한 문제에만 적용 가능하며, 현실 세계의 문제를 fit하는 데 한계 있음
• Non-parametric (비 모수적)
• 매핑 함수에 대해 strong assumption을 전제하지 않음
• kNN, 결정 트리(CART, C4.5), SVM
• 여러 형태의 함수 형식을 취할 수 있으며, 사전 전제 조건을 많이 설정할 필요없으며, 예측 성능이 높은 편
• 학습에 많은 데이터를 필요로 하며, 상대적으로 학습 속도가 느리며, overfitting 가능성 있음.

Unsupervised Learning

• Unsupervised learning 기법은 Class label이 존재하지 않기 때문에, 유사한 패턴을 가진 것들을 뭉치는(군집 분석) 방식에 이용됨
• Parametric: 혼합모델
• 내포된 클래스-조건적인 밀도(density)를 모수적 밀도의 혼합 모델로 파악하여 모델의 파라미터를 추정하는 방식
• 예: GMM
• Non-parametric: 군집화
• 내포된 density에 대한 어떠한 가정도 하지 않는 대신, 자료를 clustering을 통해 구분
• 즉, 비슷한 성격의 데이터들을 묶어나가는 방식으로, 반복적으로 모델을 수정해나가면서 최적의 군집을 찾음

Clustering

• Unsupervised learning 분야에서 가장 활발히 연구되는 분야
• optimization function을 (1) 거리 기반으로 세우고 그것을 푸는 알고리즘(k-means)과 (2) 확률과 확률분포를 기반으로 세우고 그것을 푸는 알고리즘(GMM, EM)
• 참조 블로그: http://sanghyukchun.github.io/69/
• 예: k-means
•  k-means는 데이터들 간의 거리가 가까운 k 개의 중심점(central point)으로 뭉쳐나감
• 안타깝게도 K-means는 global optimum에 수렴하지 않고 local한 optimum에 수렴하므로 initialization에 매우 취약하다는 단점을 갖는다.

$$ J=\sum_{n=1}^{N}\sum_{k=1}^{K}r_{nk}\left \| x_n-\mu_k  \right \|^2 $$

, where $r_{nk}=1$ (if $k=argmin_{j}\left \| x_n-\mu_j \right \|^2$), $r_{nk}=0$ (otherwise).

Gausian Mixture Model (GMM)

• 가우시안 혼합 모델
• 기존의 가우시안 분포들을 서로 묶어 복합적인 분포(Mixture Distribution)를 표현하고자 함; 여러 개의 가우시안 분포의 선형 결합.
• 일반 가우시안 확률분포는 데이터들의 평균을 중심으로 하나의 그룹으로 unimodel만 가능한 제약이 있으므로, 보다 일반적인 형태를 표현하기 위해, 여러 개의 가우시안을 합하여 만든 모델임 
• 즉, 데이터는 여러 군집에 속할 수도 있으며, 각 군집에 속할 확률이 다르다.
• 주어진 데이터가 어디 가우시안에서 생성되었는 지 알 수 있고, 각 가우시안이 선택될 확률과 가우시안들의 파라메터를 추정할 수 있다. 
• GMM의 performance measure는 log likelihood function, lnp(X|θ)이며, 주어진 paramter에 대해 데이터 X의 확률을 가장 크게 만드는 parameter를 찾는 것이 목표임
• 참고: MLE (maximum likelihood estimation)
• GMM을 풀기 위한 방안 중의 하나인 EM(Expectation-Maximization) 알고리즘의 적용: EM은 통계적 방법을 이용해서, 군집에 속할 확률이 가장 높은 것들끼리 뭉쳐나감.
• 즉, 주어진 파라미터를 이용해서 가장 expectation이 높은 latent variable 값을 찾아내며, 이를 이용한 값을 maximize하는 파라메터를 찾는다.
• 주어진 데이터를 군집으로 클러스터링하기 때문에, k-means 목적함수를 풀어나가는 방식을 사용 가능; 임의의 중심점을 설정하여, 군집화하고, 다시 중심점을 갱신하여 군집하는 과정을 반복하여, 적당히 수렴할 때까지 수행.
• 참조: http://sanghyukchun.github.io/70/

distance, similarity

Distance

• Distance as a dissimilarity measure
• References
• https://en.wikipedia.org/wiki/Distance
• http://rfriend.tistory.com/199
• Manhattan distance = Chebyshev distance
• Euclidean distance 
• Minkowski & r=2
• p-norm distance
• Standarized distance = Statistical distance 
• euclidean distance / standard deviation
• Mahalanobis distance
• https://en.wikipedia.org/wiki/Mahalanobis_distance

TensorFlow

TensorFlow

Reference

• https://developers.googleblog.com/2017/02/announcing-tensorflow-10.html
• Blog
• https://github.com/tensorflow/tensorflow/releases/tag/v1.0.0
• Source Code
• https://www.tensorflow.org/
• Official Site
• https://hunkim.github.io/ml/
• 기본적인 머신러닝과 딥러닝 강의
• Exercises
• https://penglover.github.io/categories/ML/TensorFlow
• 간단한 한글 설명(MNIST).
• http://pythonkim.tistory.com
• 간단한 예제들.
• http://pythonkim.tistory.com/38: tensorboard 설명
• http://pythonkim.tistory.com/56: ConvNet 설명
• https://github.com/aymericdamien
• 좋은 예제 및 참고 코드들.
• https://goo.gl/ka4Pn6
• Mnist 관련 수행 코드, 우분투에서 tensorflow/GPU 설정.
• http://goodtogreate.tistory.com/entry/CNN-for-CIFAR10
• Tutorial
• CS 20SI: Tensorflow for Deep Learning Research
• Stanford 강의. 
• 이외에도, CS229(ML), CS231n(NN) 강의 추천

Versions

Tensorflow 1.3

• As of Aug. 2017, Tensorflow 1.3 was released.

• [CPU] $ pip3 install --upgrade tensorflow
• [GPU] $ pip3 install --upgrade tensorflow-gpu

Tensorflow 1.0

• As of Feb. 15, 2017, Tensorflow 1.0 was announced.
• Python API stability
• Speedup on multiple GPUs
• tf.Keras
• Installation improvements
• [Experimental] XLA (Accelerated Linear Algebra) is a domain-specific compiler for linear algebra that optimizes TensorFlow computations. 
• XLA currently supports JIT compilation on x86-64 and NVIDIA GPUs; and AOT compilation for x86-64 and ARM.

TFlearn guide

• https://chatbotslife.com/deep-learning-in-7-lines-of-code-7879a8ef8cfb?imm_mid=0f1262

TensorFlow Installation (GPU)

• 설치 환경(2017.05.30)
• Ubuntu 16.04; python3.5.2
• 공식 홈페이지: https://www.tensorflow.org/install/install_linux
• 현재 지원버전: CUDA 8.0, cuDNN 5.1
• 선택한 설치 방식: native pip
• 1) CUDA 라이브러리 설치(v8.0)
• https://developer.nvidia.com/cuda-downloads
• linux -> x86_64 -> Ubuntu -> 16.04 -> deb(network)
• 파일 다운로드 후 관련 명령어 수행
• 2) cuDNN 다운로드(v.5.1)
• https://developer.nvidia.com/cudnn
• Nvidia 개발자 계정 필요
• 다음 명령 실행
• $ tar xvzf cudnn-8.0-linux-x64-v5.1-ga.tgz
• $ sudo cp -P cuda/include/cudnn.h /usr/local/cuda/include
• $ sudo cp -P cuda/lib64/libcudnn* /usr/local/cuda/lib64
• $ sudo chmod a+r /usr/local/cuda/include/cudnn.h /usr/local/cuda/lib64/libcudnn*
• 3) 다음 명령 실행
• $ sudo apt-get install libcupti-dev
• 4) pip3 설치
• $ sudo apt-get install python3-pip python3-dev
• $pip3 -V
• 5) tensorflow-gpu 설치
• $ pip3 install tensorflow-gpu # Python 3.n; GPU support
• $ python3 -c 'import tensorflow as tf; print(tf.__version__)'
• 기타
• 실행시 SSE, AVX 등 warning 발생하는 것은 신경쓰지 않아도 됨. TF 소스 자체에서 build하면 해결된다고 하나, 굳이 놔두어도 상관없을 듯.
• 상기 설치 후 system restart 한 번 해주면, graphic driver 잘 잡힐 듯.
• IDE로는 py-charm 등 이용.
• Performance Guide
• NCHW image data format
• Winograd conv algorithm 설정(3x3 행렬연산을 위한 tensor 성능 개선)
• $ export TF_ENABLE_WINOGRAD_NONFUSED=1
• # Couldn't open CUDA library libcupti.so.8.0. LD_LIBRARY_PATH
• $ export LD_LIBRARY_PATH=/usr/local/cuda/extras/CUPTI/lib64:$LD_LIBRARY_PATH

Library

• tf.Transform
• ML 전처리를 위한 TensorFlow 라이브러리 (Beam Preprocessing).
• Users define a pipeline by composing modular Python functions, which tf.Transform then executes with Apache Beam, a framework for large-scale, efficient, distributed data processing. --> 그렇다면, 런타임(Serving)에 전처리를 위해서는 Apache Beam을 별도로 설치해야 하나? 
• tf.Transform allows users to compute summary statistics for their datasets.
• Edward
• 확률 모델링, 추론을 위한 라이브러리.